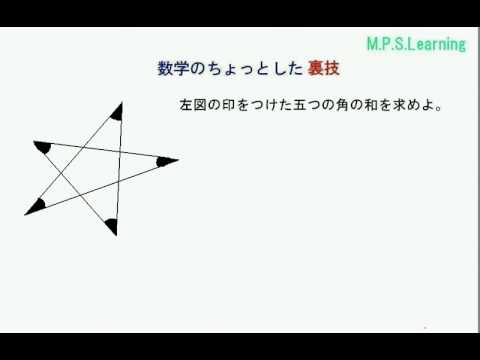
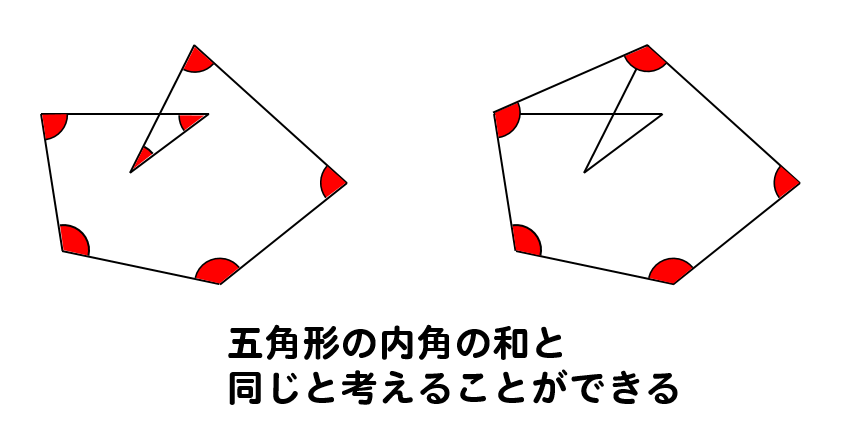
三角形の数で内角の和が計算できます 五角形と六角形の内部に作成できる「三角形の数」「内角の和」は下の図の通り。 どうですか? ここまではそれほど難しくないと思います。 多角形と言っても、まだまだ五角形、六角形と数が少ない形ですからね。 ということで! ここで一気に「百角形」の内角の和を求めてみましょう。 びっくりだと思いますが、下に 下の添付図の赤線のように考えると、赤で示す角度の和は360°です (多角形の外角の和)。 同様に青の合計も360°です。 7個の三角形の内角の和は180×7=1260°です。 従って求める答えは =540° 以上です。2-4-1 星型多角形の内角の和 教材(問題場面) 図のように5つの点A,B,C,D, Eがある。点Aから左回りに1つとば しで点を順に結んでいくと星形五角形 ができる。その内角(∠a~∠e)の和 をいろいろな方法で求めてみよう。 H 活動α3 点が一直線上になる。頂点が内部に入る。 G c ∠a

多角形とは 内角の和の求め方を簡単に解説 高校生向け受験応援メディア 受験のミカタ
多角形の角度の求め方
多角形の角度の求め方-求めたい箱の仕上がりは、角度=β です。板の厚み・幅は関係ありません。その場合の、幅側(α)と、厚み側(X)の角度の求め方です。ただし、関数電卓がないと大変です。 角度 α は、Tan1 (アークタンジェント) Sin β 角度 X は、Tan1 (アーク たしか、角度の求め方って何か法則があったよね? というわけで、今回の記事では「多角形の内角の和の求め方」について解説していきます。 かず先生 六角形の内角の和は7°になるよ これは、ある法則を身につけておくと簡単に計算できるよ! スポンサーリンク Contents 1 多角形の




星形の角度 内角の和の求め方を問題解説 数スタ
②正多角形のかき方 ③円周率の求め方(円の円周と直径の関係) ④円周や直径の求め方 ⑤生活の中で円周を求めるよさ 教え方1 正六角形や正八角形を作らせながら、正六角形や正八角形の意味をとらえさせます。 動画を見せて六角形のつくり方を説明し、 お子さんに作らせて、 気づいたこと 頂点の数「n」でわると正多角形の1つの内角の大きさになるよ。 180× (n2)/n どの内角も同じ大きさだからね! まとめ:正多角形の内角は「総和」を「頂点の数」でわれ! 正多角形の内角の公式は、 180°×(n2)/n だったね。 ようは、 平面図形基礎 小3からプリント12枚! 正・直角・二等辺三角形の三角形の角度・長さから面積まで中学受験まで 「三角形は知ってるけど、何を勉強するの? 」という小3から「応用問題を解きたい」という中学受験生の方へ。 基本から発展まで東大
・星形六角形の頂角の和は,ほとんどの生徒が求めている。 <発表された生徒の解き方> (4) レポート作成の課題を与える。 1) 頂角の和が180度になる星形多角形を調べよう。 2) 星形偶数多角形の性求角と方程式 角度を求めることは、小学生のころにもやっていることです。 しかし、角度を求めるために方程式を用いることは中学生ならではです。 そんな問題を練習しましょう。 例題1 次の図の角 \(x\) の大きさを求めなさ 例題1 下の図のように三角形の外角の定理を利用して考えると、 ア+ウ=キ、イ+エ=カより、ア+イ+ウ+エ+オ=カ+キ+オ= 180° となります。 下の図のようにブーメランの定理を利用して考えると、 ア+ウ+エ=カ、また対頂角は等しいのでカ=キとなり、ア+イ+ウ+エ+オ=イ+オ+キ= 180° となります。
上の事実は次のように説明できます. まず, 多角形の各頂点における内角と一つの外角の和は常に 180° 180 ° なので, n n 角形の内角と外角の和の合計は, 180°×n 180 ° × n です.そして, n n 角形の外角の和は,これから内角の和をひいたものなので, 180星形多角形の内角とは,多角形 の各辺の延長線でつくられた, 鋭角のみをいいます。 ∠a+∠b+∠c+∠d+∠e を 星形五角形の内角といいます。 星形多角形の内角 星形多角形 2 星形五角形の角の和を求めよう(∠a+∠b+∠c+∠d+∠e) 正多角形の内角の大きさを求める 授業のねらいは、「内角の大きさを計算で求めて、プログラミングを使って正多角形を作図しよう」です。 まず、正三角形の1つの内角の大きさの求め方を確認します。 先生と児童のやりとりは次の通りです。 先生が



多角形の内角の和は 1分でわかる公式 問題の求め方 簡単な証明




多角形の内角の和 は何度なのか を説明します おかわりドリル
正多角形の内角・外角の求め方を解説! 星形の角度の求め方を解説!←今回の記事 ブーメラン型の角度の求め方! ちょうちょ型の角度の求め方を解説! 合同な図形の基本性質とは? 三角形の合同条件を使って、合同な三角形を見つける方法! (2) 多角形の外角の和の公式より、 多角形の外角の和は、常に \(360^\circ\) であるので、 正九角形であるとき、\(1\) つの外角の大きさは \(360^\circ \div 9 = 40^\circ\) 答え: \(40^\circ\) (3) 多角形の対角線の本数の公式より、 \(\displaystyle \frac{n(n − 3)}{2}\)四角形,五角形,六角形の内角の求め方を考え,この考え方を表にまとめる活動を行う。 この活動の中で,中学1年までに学習した平面図形の三角形と角度に関する基本を確認し ながら学習するよい機会と考える。 また,作った表から一般化して,n角形の内角の和を式で表現することが要求さ



ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく
三角形が4つ、三角形の内角の和は180゚ですから 六角形の内角の和は7゚正六角形なので 内角の大きさは皆同じですからひとつの角は1゚になります。 最初に戻って n角形 で考えます。 4角形では対角線が1本引けて三角形2つに分けられます。 5角形では対角線が2本引けて三角形3つに分けられます。 6角形では対角線が3本引けて三角形4つに分けられます。 7この性質は多角形、正多角形に関係なく どんなやつでも全部合わせたら360°になります。 では、このことを使って考えると 正多角形の外角1つ分の大きさは $$\LARGE{360 \div (角の数)}$$ をすることによって求めることができます。 正三角形の場合角というのは、直線や線分が交差した点と、その両端の線で挟まれた部分のことを言います。 多角形はどのように区別がされているかというと、この角の数によってされています。 左から「三角形」「四角形」「五角形」です。 また、図形の内側の角を 内角 といい、それから延長した辺と1辺がつくる角を 外角 といいます。 この2つの角度を足すと 180° になり




角度の計算 裏技まとめ 教遊者




星形の角度 内角の和の求め方を問題解説 数スタ
三角形の内角の和は、全ての 多角形 たかっけい の角度 を 角の大きさの表し方(角度)を理解する。 また、直線が交わったときにできる角の大きさを求められ、垂直と平行を理解し、平行な直線のせいしつを使って角の大きさを求める。 分度器に使い方と三角定規の性質と特徴 4年生 下の図のように、2本の直線が交わっています。a、b、cの角の大きさは、それぞれ何度になるか求めなさい。 解説 まずbの角度から求めていきます。向かい合った角、つまり対頂角は等しいので、b=30° 次にaの角度を求めます。直線の角の大きさは180°です。そのためaの角度はやじり形の角度や多角形の内角の計算を利用したりして求めるなど、既習の図形の性質を使い、根拠を明らかにして説明する ことができる。 本時の展開(7/13時) 過程 学 習 活 動 評価について 指導・援助 つ か む 表ができるように 深 め る 性質を使うと、 ・自分の考えと似てい 星型の




多角形の内角の和 は何度なのか を説明します おかわりドリル
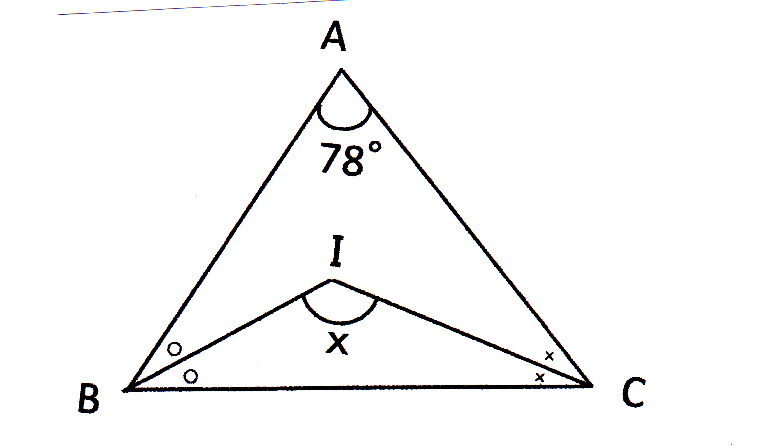



三角形内の角度を求める問題 現役塾講師のわかりやすい中学数学の解き方
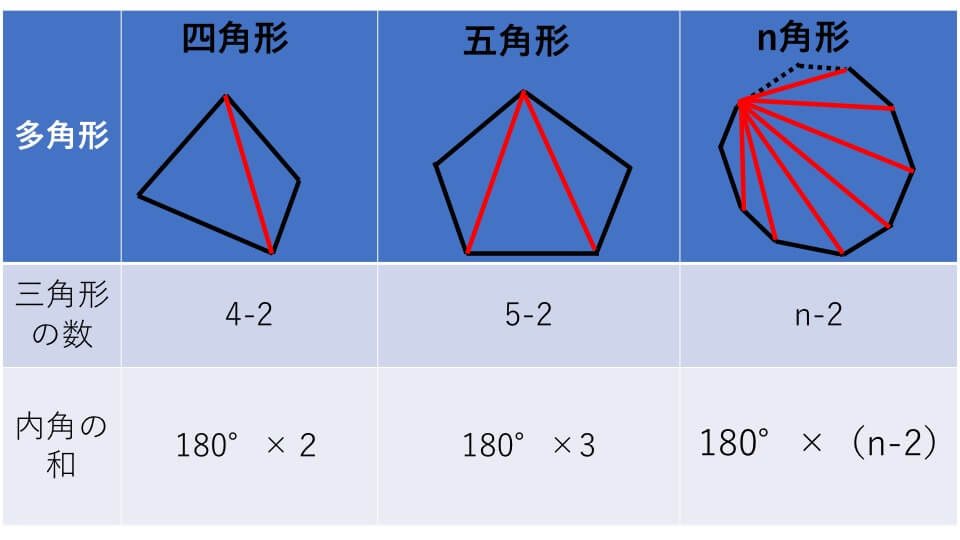
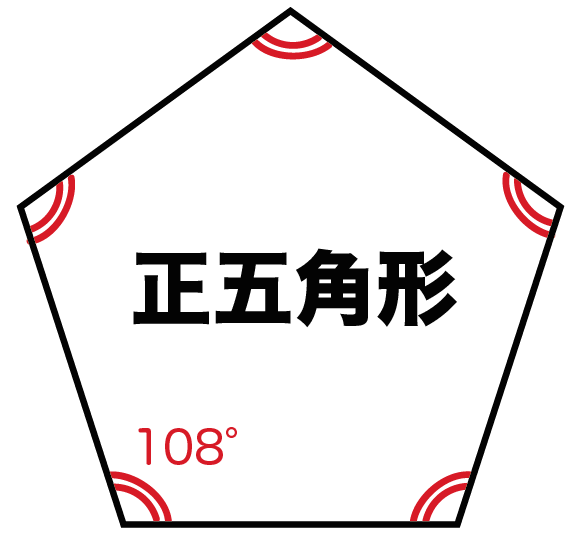
角が 1 1 つ増えるたびに三角形の数も 1 1 つずつ増えていくのが分かりますね。 n n 角形の内角の和は「 180°× (n− 2) 180 ° × ( n − 2 ) 」でしたが、「 n− 2 n − 2 」というのは分割できる三角形の数と見ることができるのです。 そしてそれぞれの多角形の内角の和はすべての三角形の内角の和と等しいので、 「180° 180 ° ×(三角形の数)」 というのが c 多角形。 t 直線だけで囲まれた図形,曲がった線はあかんで。 子どもたちの多くは,自分のノートにメモした。 続いて,本時の課題へと移る。 t それでは問題です。今日は五角形の角の和を求めます。五角形の角の和ってわかるかな?正多角形の角度の求め方は? 正多角形の1つの角度θの求め方(計算式)を下記に示します。nは正多角形の辺の数です。 正六角形の辺の数は6なのでn=6です。よって、 となります。正多角形の角度の求め方は下記も参考になります。 正多角形の角度は?1分でわかる値と計算式、正6角形、正9角形の角度
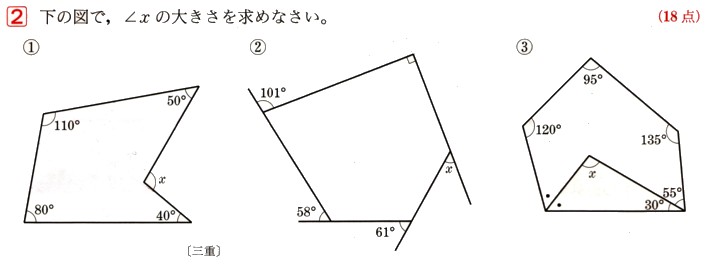



中学2年数学 図形の調べ方 三角形 多角形と角 確認問題2 解答 あんのん塾
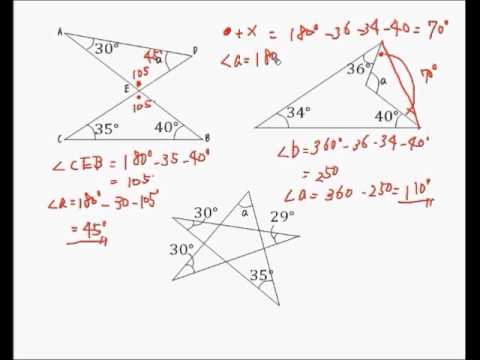



多角形から角を求める Youtube
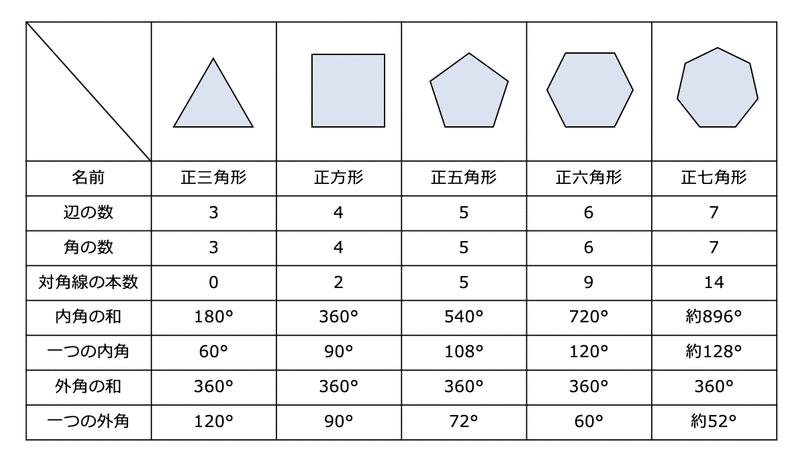
正多角形(せいたかっけい、せいたかくけい、regular polygon)とは、全ての辺の長さが等しく、全ての内角の大きさが等しい多角形である。 正多角形は線対称の図形であり、正 n 角形に対称軸は n 本ある。 また、正偶数角形は点対称の図形でもある。 辺の数が同じ正多角形どうしは全て互いに小学校5年生で習う「多角形の内角の角度」 を求める問題集です。 問題をランダムで生成することができ、答えの表示・非表示も切り替えられます。印刷してご活用ください。 ちなみに多角形の内角の角度の求め方についてはこちらに詳しく説明しています。等しい多角形を正多角形といいます。 13 正答例と解説 5年「正多角形と円周の長さ」 〔考え方のポイント〕 正六角形の性質を使って円周の長さを求めよう 答え( イ・エ ) 円の中心のまわりを,グループの数で等分した正多角形を考 えます。



1




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
外角の求め方 外角の求め方を下記に示します。 外角=外角と隣り合わない内角の和 例えば下図の三角形の外角=3050=80度です。上式を覚えておけば簡単に外角が算定できます。 なぜ外角=外角と隣り合わない内角の和となるか解説します。三角形の内角の和は180度です。角度の大きさをa、b、cとします。このとき 簡単公式平行四辺形の角度の求め方がわかる3ステップ 中2数学 他の星型多角形も内角の和は180度になるんですか? Ken より 19年1月6日 7 AM 星の角が5つだったらそうなるね! ミー より 19年1月26日 959 AM 御回答、ありがとうございます! 質問する コメントをキャンセル コメント角測量とは、対象物相互間の角度を求めるための測量で、平面方向の水平角と高さ方 向の高度角があり、測角儀(角度を測る測量機器)は、トランシット、セオドライト、 トータルステーションなどに代表される。図-1に角測量の例を示す。 図-1 角測量の例 角度の基本的な計測方法は
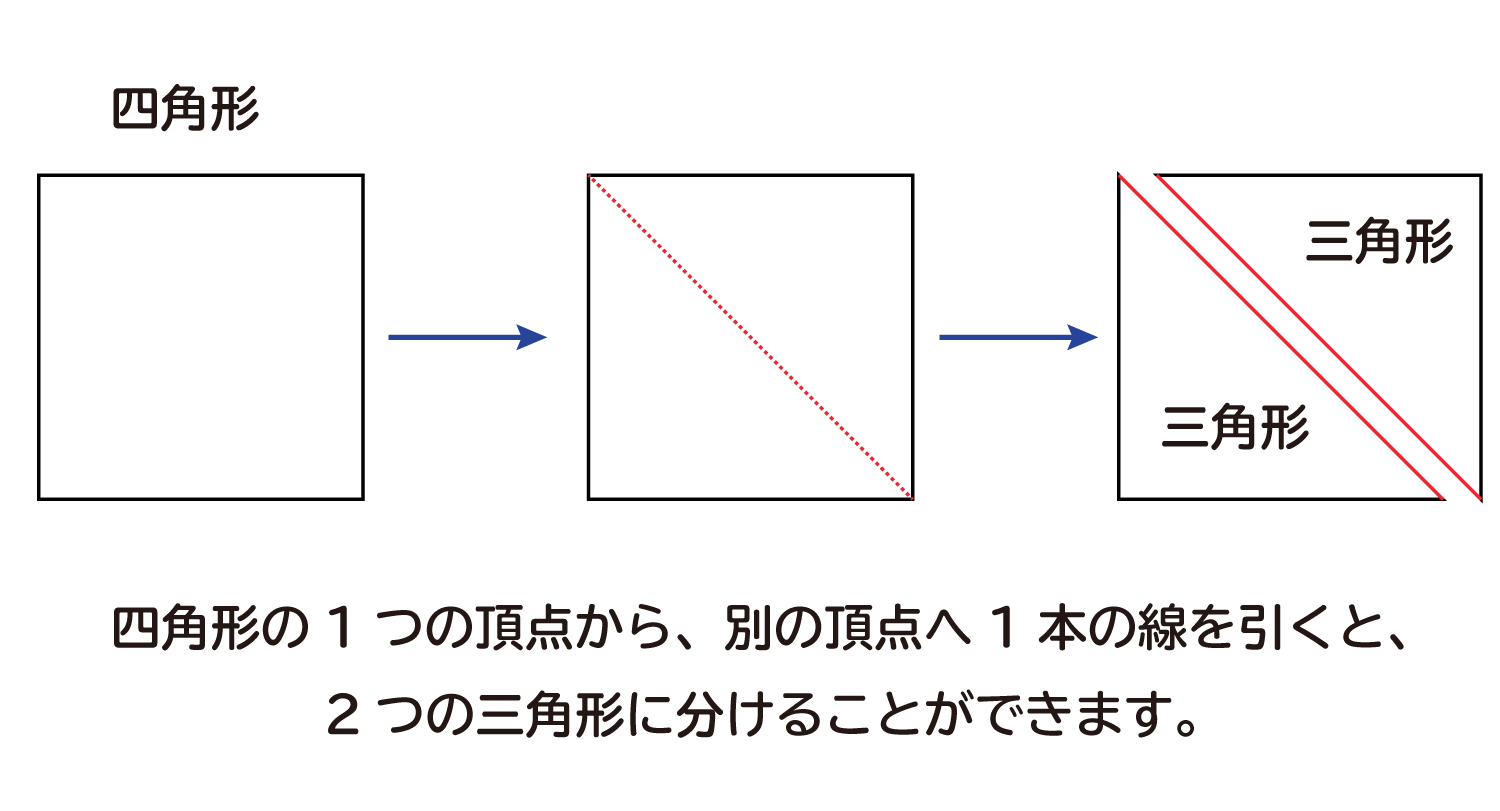



多角形の内角の和 は何度なのか を説明します おかわりドリル
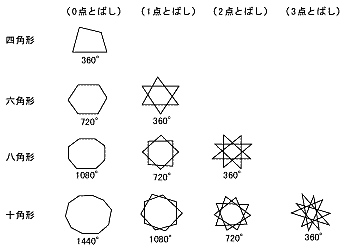



課題学習の指導 数学
以上のことから、多角形の内角の和は下の 公式 で求められます。 多角形の内角の和 = 線を引いて現れた三角形の数 × 180 これをもっと簡単な公式にします。 上の図をると、三角形の数は多角形の角の数より2つ少ないことがわかります。



多角形の角度 Youtube



中学受験 算数 角度 基礎からわかりやすくポイント解説 中学受験アンサー



実践例 プログラミングで正多角形を学ぶ 山崎智仁 Tomohito Yamazaki Note




中2数学 ブーメラン型角度の求め方を解説 数スタ




小学校5年 算数 正多角形の角の大きさ Youtube




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学
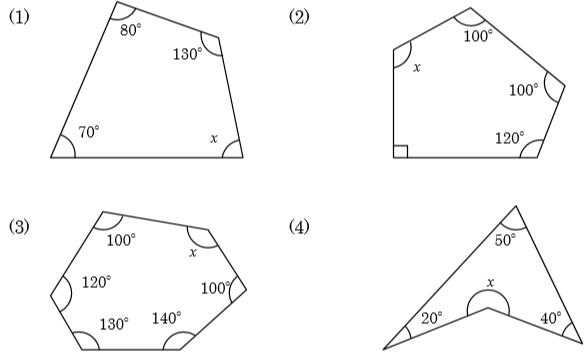



中2数学 多角形の内角の和と外角の和のポイントと練習問題 Pikuu
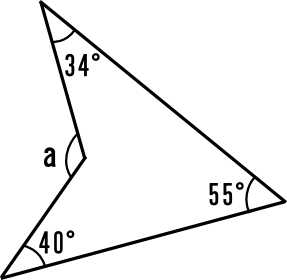



中学2年数学練習問題 図形の調べ方 多角形の内角と外角の解答




正多角形の内角と外角の大きさ 具体例で学ぶ数学
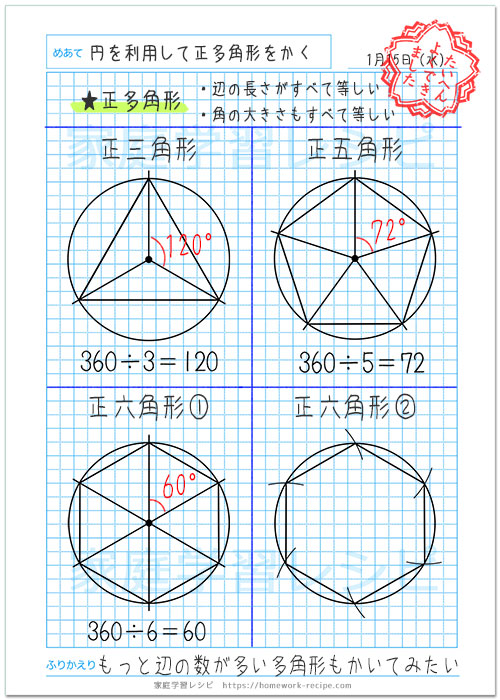



円を利用して正多角形をかく方法 算数の自主学習 家庭学習レシピ



中学二年生の星形五角形の内角の和の求め方を教えてください 星 Yahoo 知恵袋



Q Tbn And9gctqxnxegjdxp Adpruavnpmf2sansioyhqkmwlqdbcw Fiiw67x Usqp Cau
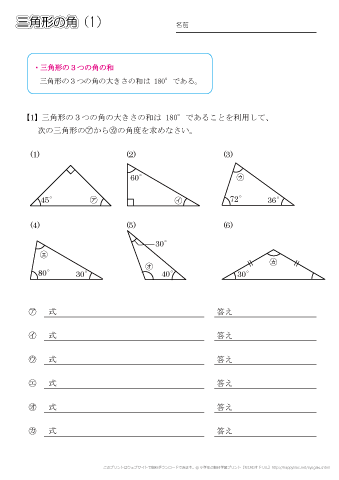



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




多角形の角度の和の求め方 添付画像の黒い印の角の角度の和を求めたいのです Okwave




内角の和から多角形を求める方法と一覧表 具体例で学ぶ数学
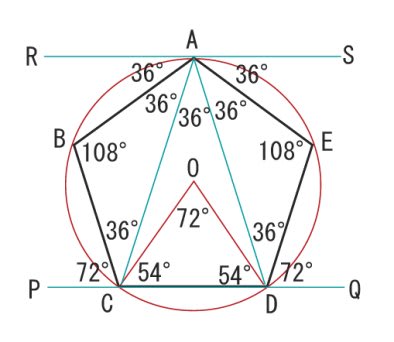



正五角形というだけで 分かる角度は 名寄 算数数学教室より




内角の和の公式 内角の和が1800 の多角形は何角形 中学や高校の数学の計算問題



多角形の内角と外角 思考力を鍛える数学




多角形の角度 添付した図形の Bgeの大きさを求めます 行き詰まっていま Okwave




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく
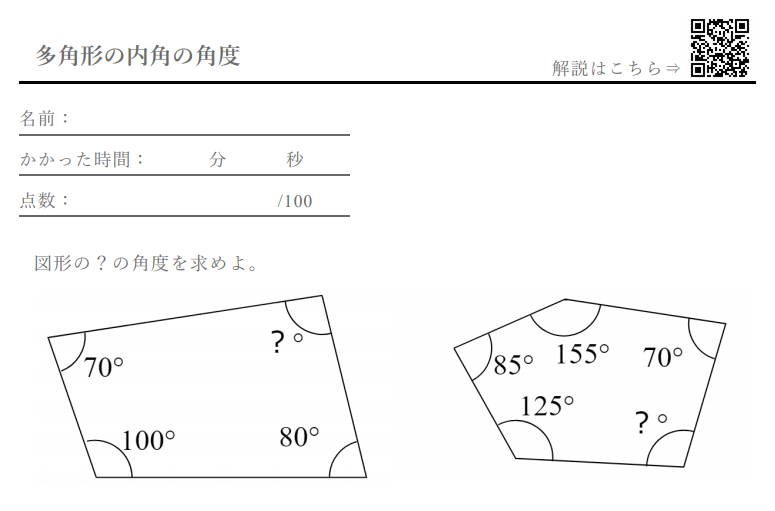



多角形 の内角の角度 計算ドリル 問題集 数学fun




多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト
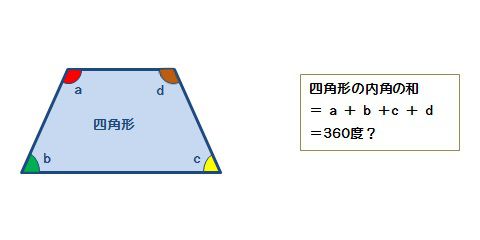



四角形の内角の和 算数の公式覚えてますか




多角形の性質 中学受験準備のための学習ドリル




多角形の角 無料で使える中学学習プリント
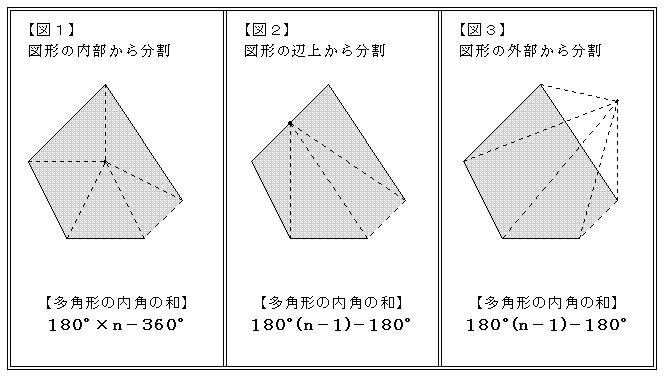



多角形の角




課題学習の指導 数学



ちょうちょ型図形の角度は 求め方を徹底解説 数スタ




正多角形の 内角が あっという間に分かる術 名寄 算数数学教室より




中学の数学の角度の問題を教えてください 中学生の息子から 添付画像 数学 教えて Goo




図形 角度 錯角 同位角 多角形の内角外角など 現役塾講師のわかりやすい中学数学の解き方




星型 角形の角度の問題 恋する中学受験 大学受験を見据えた中学受験




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学
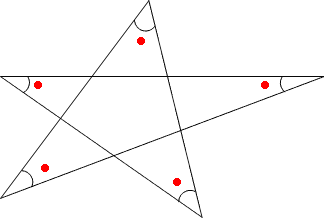



角度の求め方 算数の教え上手 学びの場 Com
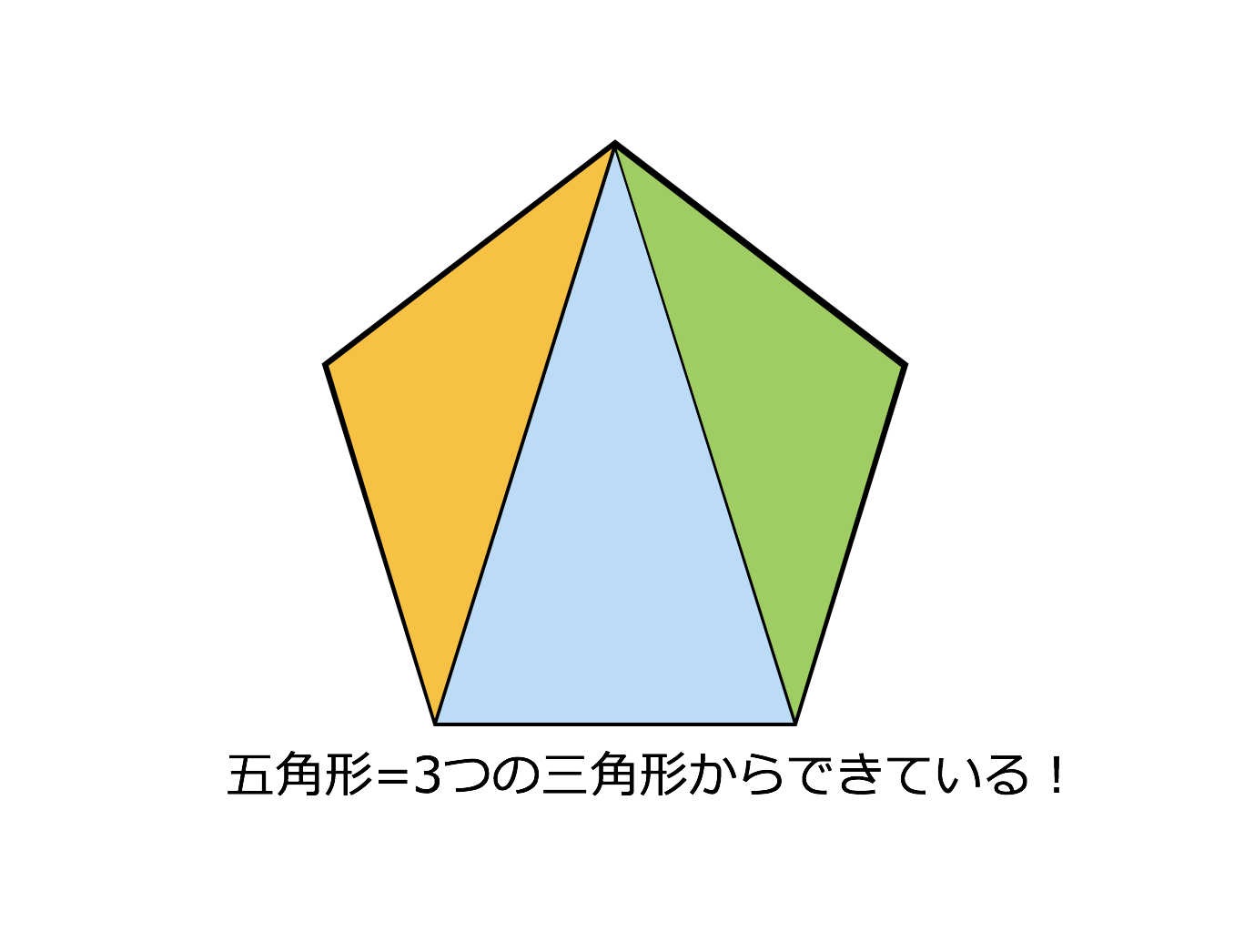



3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




分かりません 教えてください Clear




中2数学 複雑な多角形 角の和 応用問題
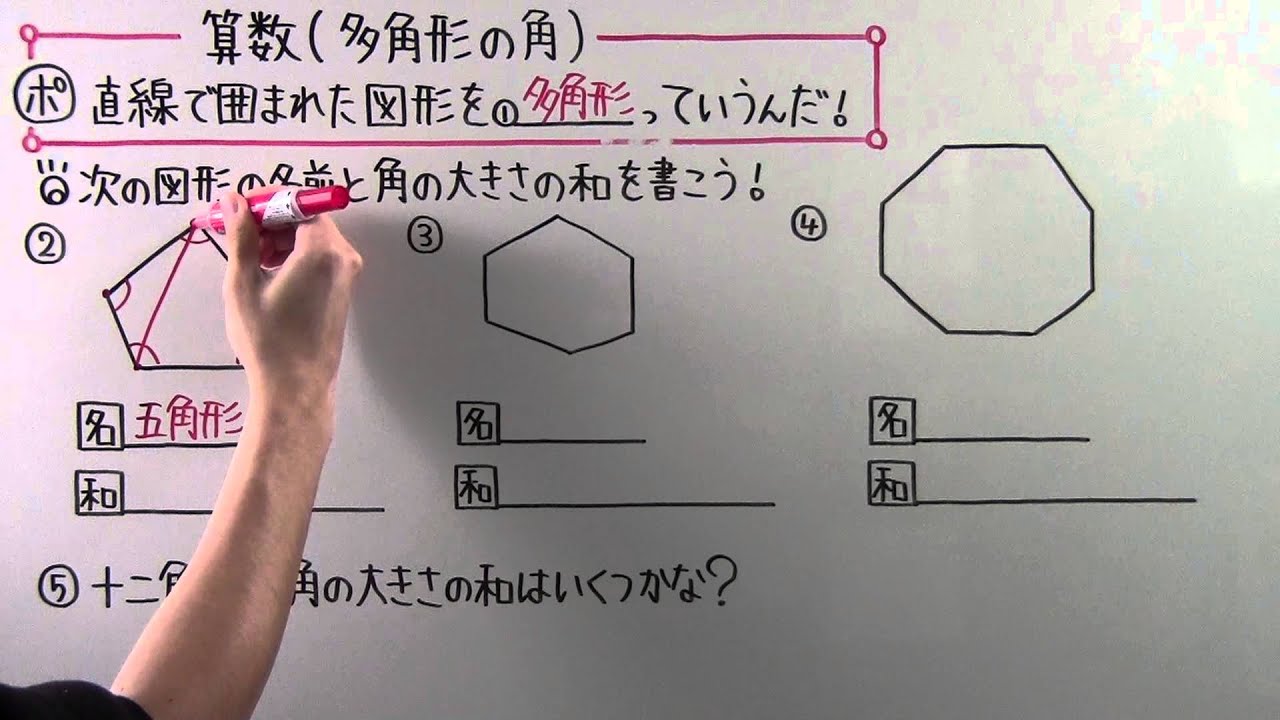



小5 算数 小5 33 多角形の角 Youtube




正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく



正n角形の内角の和は2 n 2 直角である 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ



問題1 平行線に二本の直線が交わっているとき Xの大きさを求めよう



1
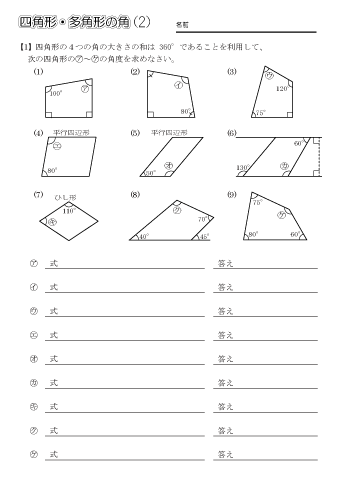



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生
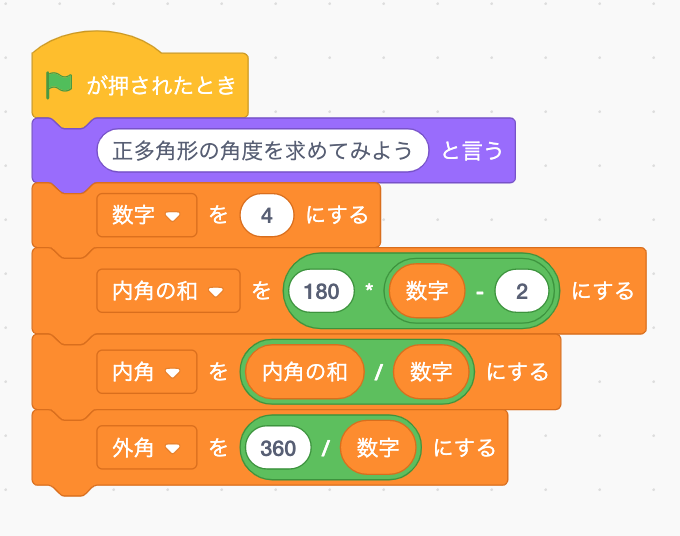



Scratch プログラミングで正多角形の内角 外角を求めてみよう いなきたものづくりラボ



正8角形です あ い う それぞれの角度の求め方を教えてください 一つの角の Yahoo 知恵袋
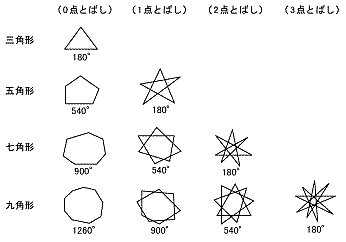



課題学習の指導 数学




多角形とは 内角の和の求め方を簡単に解説 高校生向け受験応援メディア 受験のミカタ




3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




いろいろな正多角形をかいてみよう 家庭学習レシピ
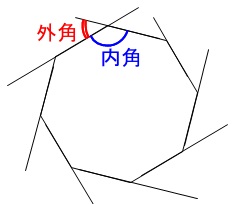



多角形の内角の和の公式と外角の和を利用した角度の求め方




図形 角度の求め方 中2 画像の図形の内角の和は900度なのですが 求め Okwave




複雑な多角形の角度の和が知りたいのですが 添付画像の16か所の黒丸部分の Okwave
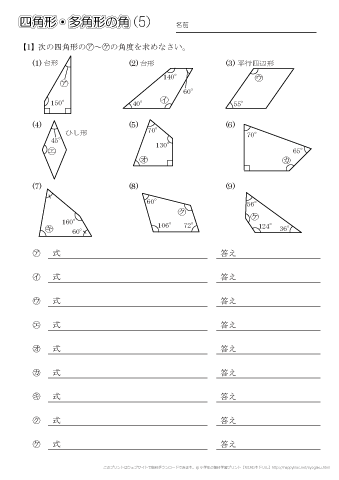



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生




多角形の内角の和 算数の公式覚えてますか
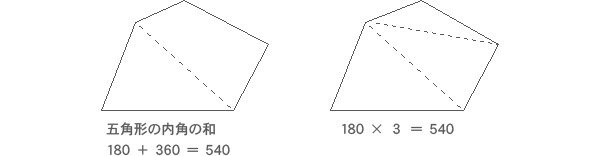



重なる形と図形の角を調べよう 第5学年 小学校 算数 My実践事例 日本文教出版




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく




中2数学 複雑な多角形 角の和 応用問題



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
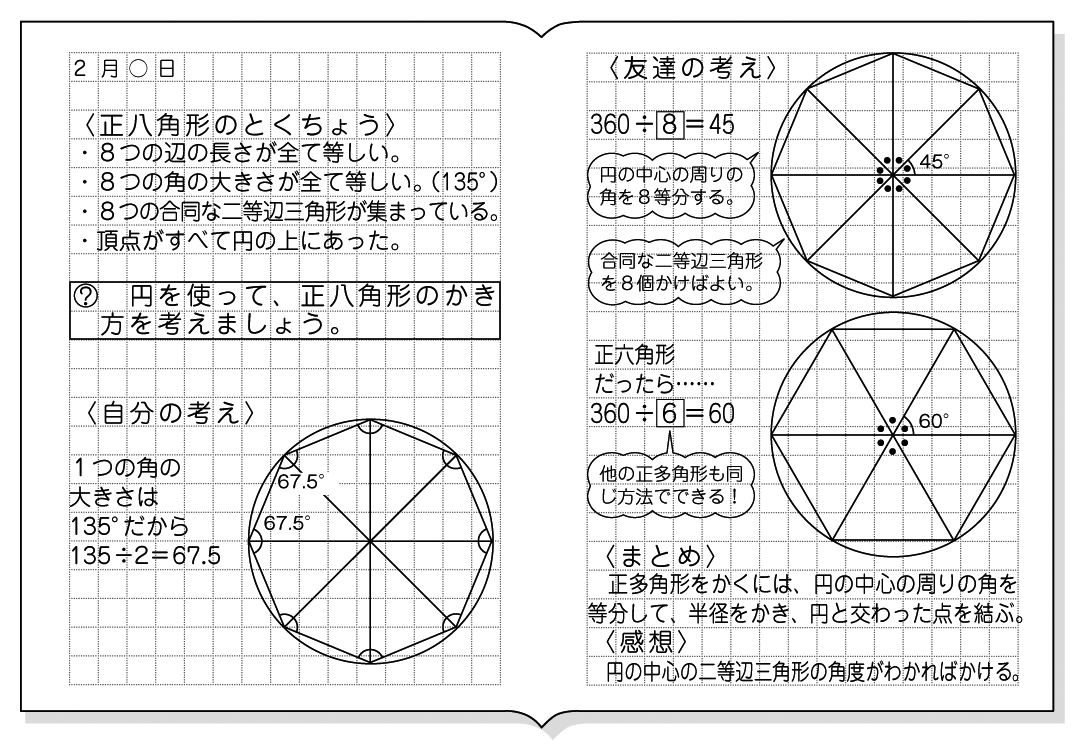



小5算数 正多角形と円 指導アイデア みんなの教育技術




内角の和 180 N 2 外角の和 360 教遊者
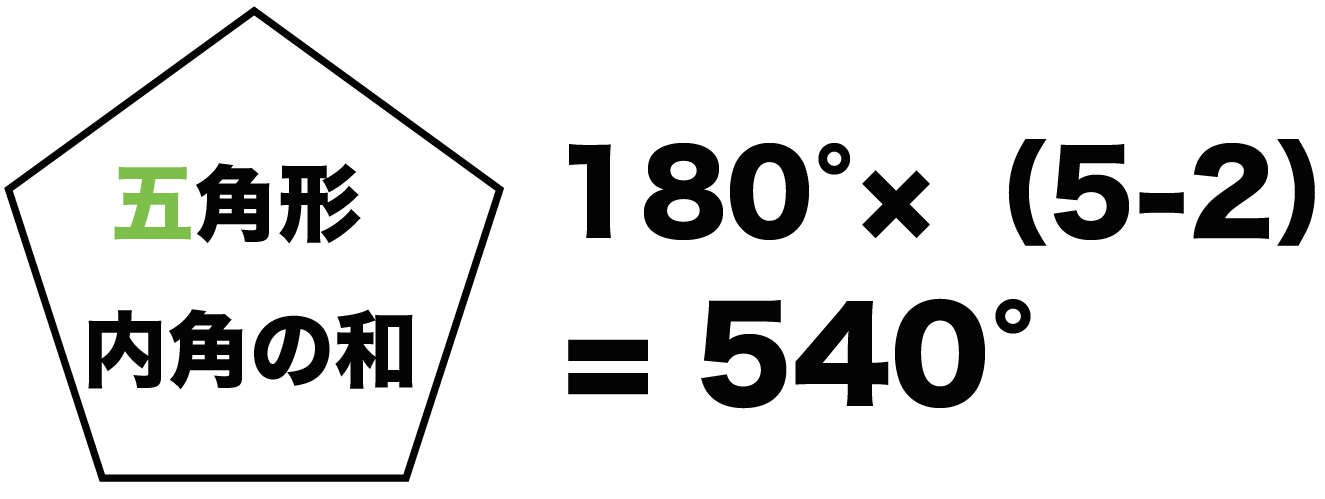



中2数学 多角形の内角の和が3秒でわかる公式 Qikeru 学びを楽しくわかりやすく



正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく
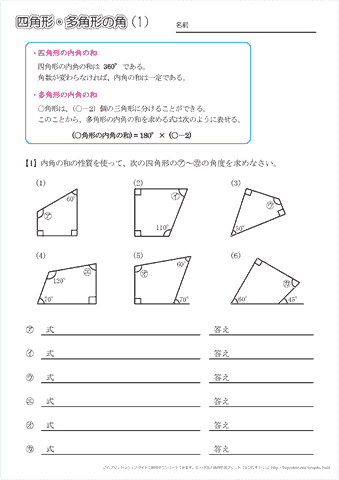



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生




内角の和 180 N 2 外角の和 360 教遊者




小5 算数 小5 54 正多角形 Youtube
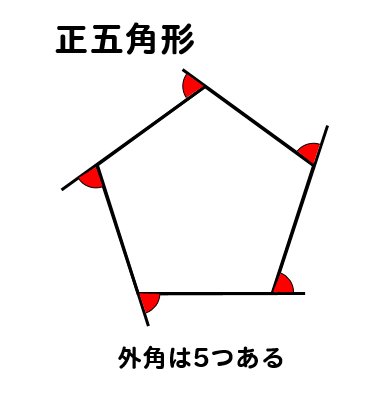



正多角形の1つの内角 外角を求める方法を問題解説 数スタ



中2の数学の多角形の問題で この図形のyの角度の求め方を教えてください Yahoo 知恵袋
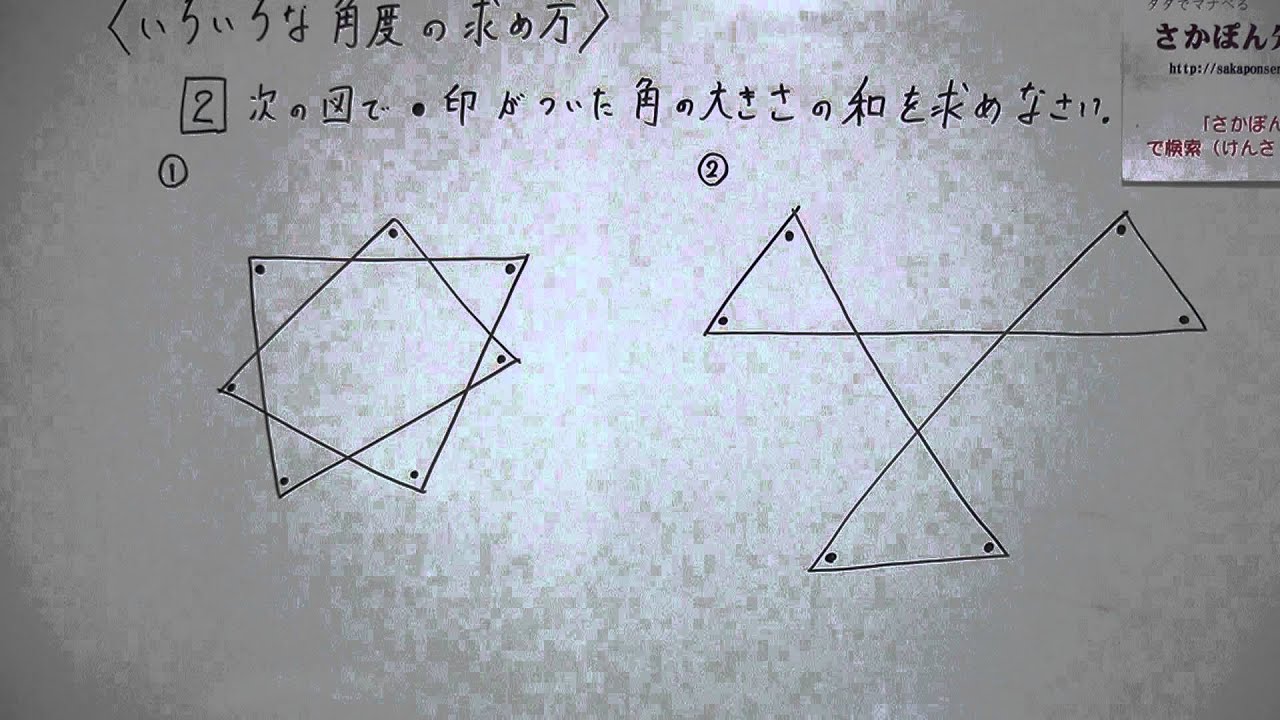



中学校2年生数学 いろいろな角度の求め方




小5 算数 小5 31 三角形の角 Youtube




小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ




内角の和 180 N 2 外角の和 360 教遊者




数学 中2 51 多角形の内角と外角の和 基本編 Youtube




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく




多角形の内角の和 外角の和の公式 数学fun




角度の求め方 算数の教え上手 学びの場 Com




分かりません 教えてください Clear




数学 中2 53 角度チャレンジ Lv 1 Youtube




内角の和 算数用語集




外角の求め方 外角の和を使って多角形の角度を求める問題 中学や高校の数学の計算問題




角度を計算する方法 9 ステップ 画像あり Wikihow
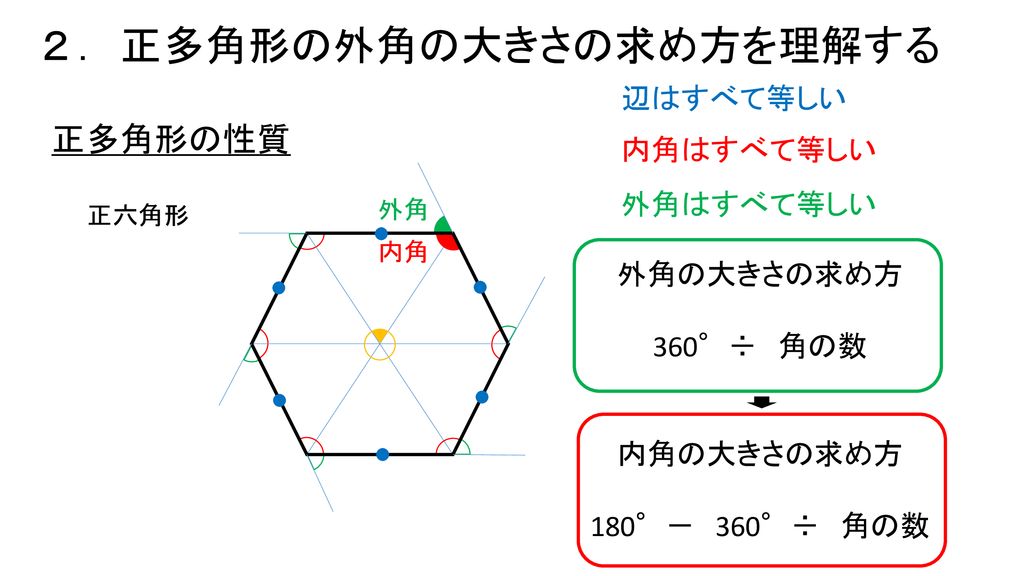



正多角形の作図 プログラミングで多角形を描く方法を考えよう 1時間目 Ppt Download




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく



1



720度 星形九角形の角度の和



0 件のコメント:
コメントを投稿